Web-Based Control System Analysis and Design
Root Locus
DESCRIPTION:
This function computes and plots root locus of an SISO system.
Normally, roots of the characteristic equation will change as one of the system's
parameters varies over a continuous range of value. Assume that the control system
shown in the figure below
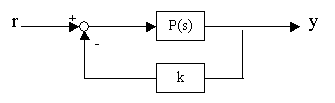 consists of the plant P(s) and the scalar gain k. The root locus is the trajectories of the roots of following equation q(s) = 1 + kP(s) when the feedback gain k varies from 0 to positive infinity.
consists of the plant P(s) and the scalar gain k. The root locus is the trajectories of the roots of following equation q(s) = 1 + kP(s) when the feedback gain k varies from 0 to positive infinity.
The number of branches of the root locus equal the number of the poles. Each branch
begins at one of the roots (poles of the system) and moves off to infinity or zeros of the system.
The poles are marked as x's and the zeros o's in the root locus plot.
Please select a model to represent the system:

